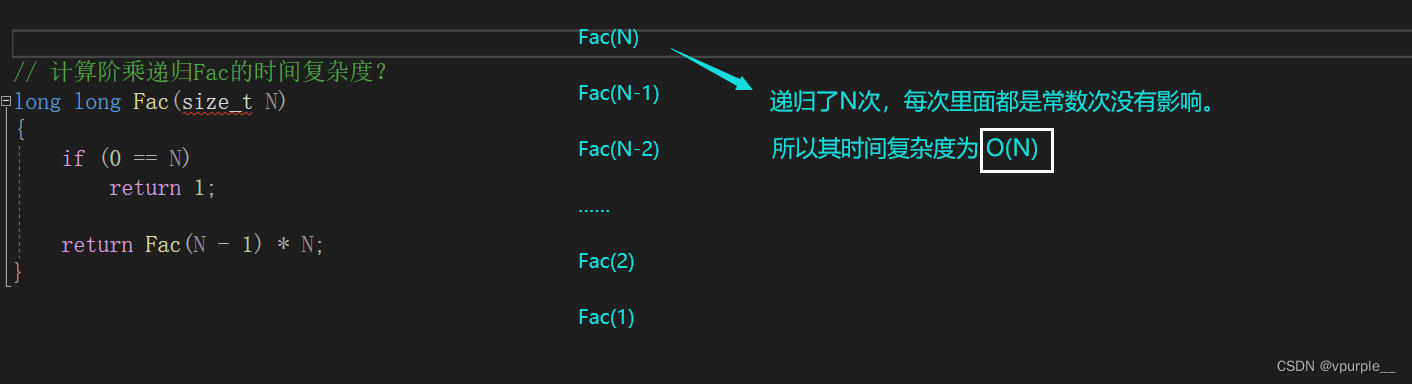
时间复杂度

发表于 分类于 阅读次数：

在学习数据结构和算法的时候，经常会碰到 O(1),O(n)等等用来表示时间和空间复杂度，那这到底是什么意思。我们对于同一个问题经常有不同的解决方式，比如排序算法就有十种经典排序（快排，归并排序等），虽然对于排序的结果相同，但是在排序过程中消耗时间和资源却是不同。

对于不同排序算法之间的衡量方式就是通过程序执行所占用的时间和空间两个维度去考量。

1 数学基础

1.1 幂函数

$y=x^k$

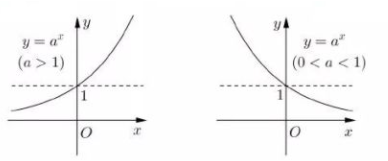
1.2 指数函数

函数$y=a^x(a>0且a\ne 1)$叫做指数函数，自变量叫做指数，a叫做底数。

1.3 对数函数

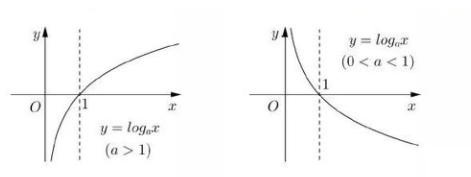
如果$a(a>0,a\ne1)$的b次幂等于N，即$a^b=N$，那么b叫做以a为底的N的对数，记做$\log_aN=b$，其中a叫做对数的底数，N叫做真数。

2 时间复杂度

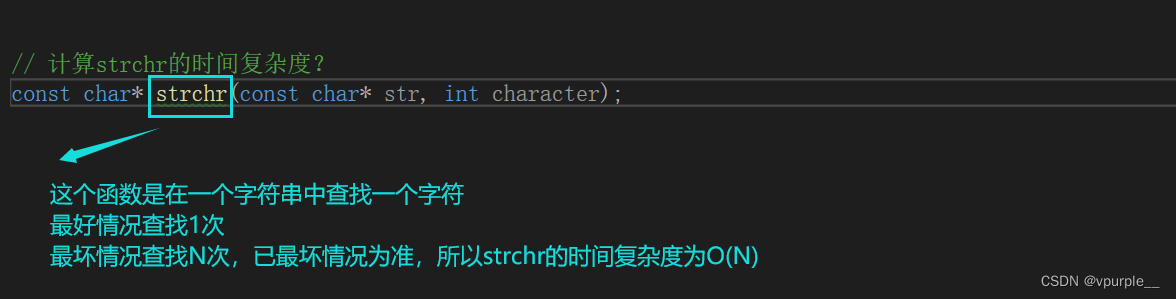
若存在函数 $f(n)$，使得当 n 趋近于无穷大时，$T(n)/ f(n)）$的极限值为不等于零的常数，则称$ f(n)$是 $T(n)$的同数量级函数。记作 $T(n)= O(f(n))$，称 $O(f(n))$为算法的渐进时间复杂度，简称时间复杂度。

简单理解就是一个算法或是一个程序在运行时，所消耗的时间（或者代码被执行的总次数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
int sum(int n) {
①   int value = 0;
②   int i = 1;
③   while (i <= n) {
④       value = value + i;
⑤       i++;
    }
⑥   return value;
}

假设n=100，该方法的执行次数为①(1次)、②（1次）、③（100次）、④（100次）、⑤（100次）、⑥（1次）
合计1+1+100+100+100+1 = 303次

上面的结果如果用函数来表示为：$f(n) = 3n+3$，那么在计算机算法中的表示方法如下。

2.1 表示方法

大 O 表示法：算法的时间复杂度通常用大 O 来表示，定义为 $T(n) = O(f(n))$，其中 T 表示时间。

即：$T(n) = O(3n+3)$

这里有个重要的点就是时间复杂度关心的是数量级，其原则是：

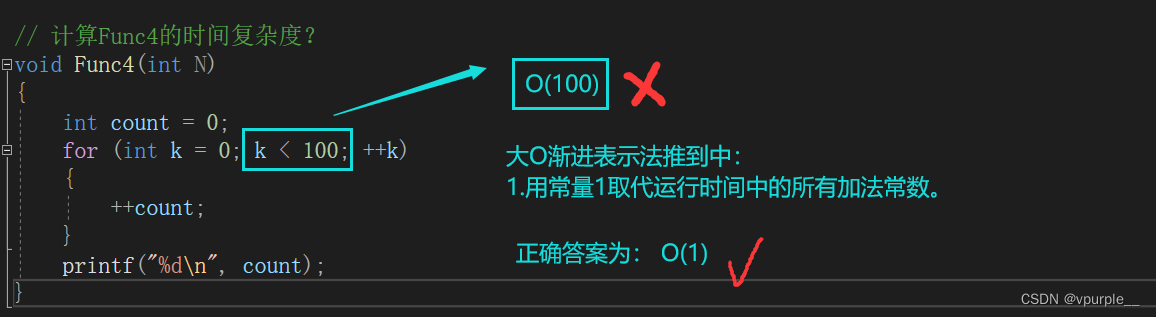
  1. 省略常数，如果运行时间是常数量级，用常数 1 表示
  2. 保留最高阶的项
  3. 变最高阶项的系数为 1

如$2n^3+3n^2+7$ ，省略常数变为 $O(2n^3+3n^2)$，保留最高阶的项为 $O(2n^3)$，变最高阶项的系数为 1 后变为 $O(n^3)$，即为 $O(n^3)$ 的$2n^3+3n^2+7$时间复杂度。

同理，在上面的程序中$ T(n) = O(3n+3)$，其时间复杂度为 $O(n)$。

注：只看最高复杂度的运算，也就是上面程序中的内层循环。

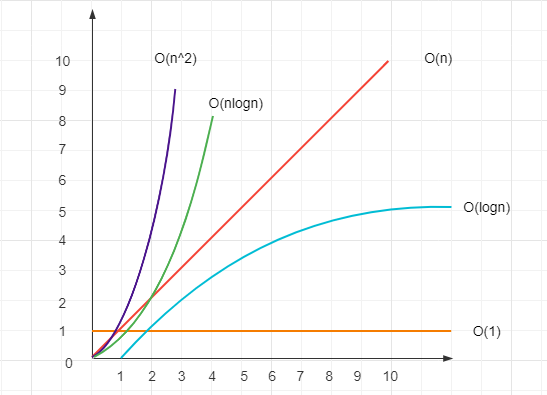
2.2 常见时间复杂度的阶

时间复杂度的阶主要分为以下几种

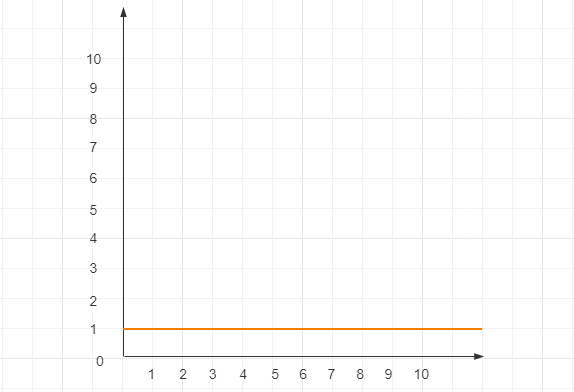
2.2.1 常数阶 $O(1)$

1
2
int n = 100;
System.out.println("常数阶：" + n);

不管 n 等于多少，程序始终只会执行一次，即 $T(n) = O(1)$

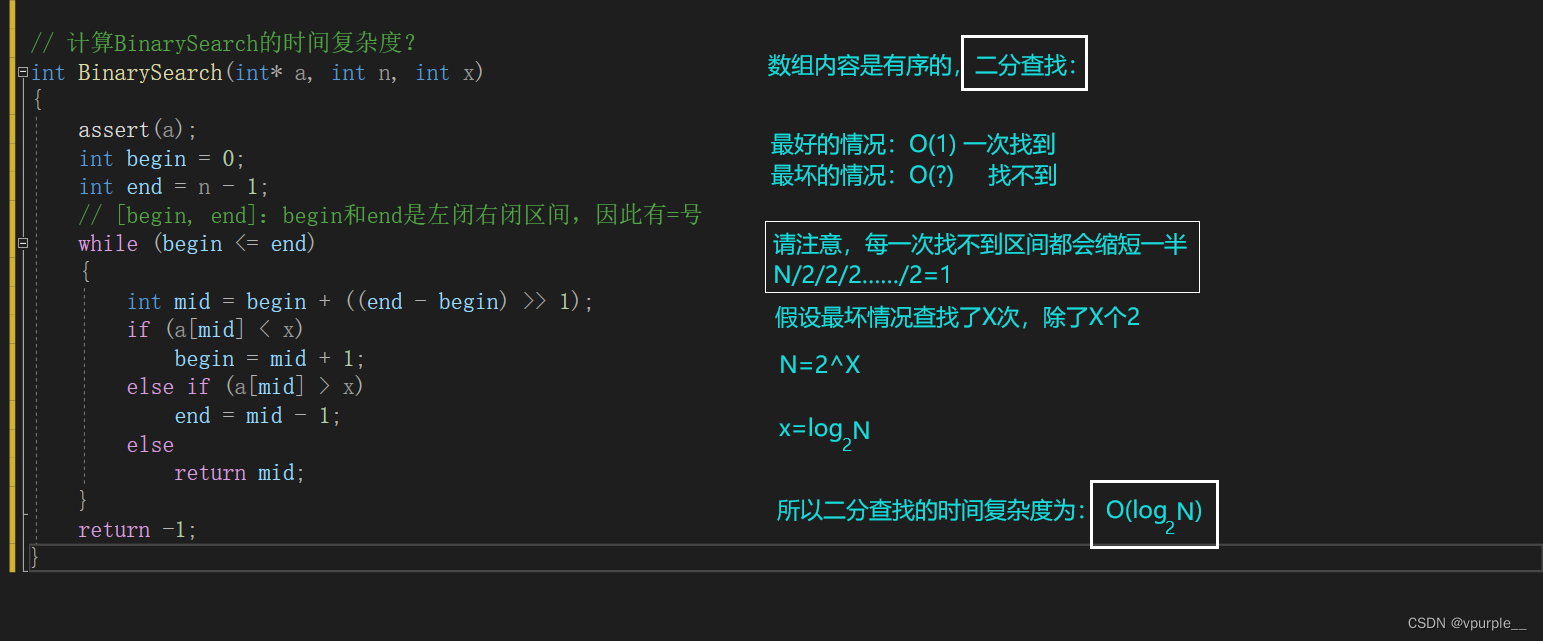
2.2.2 对数阶$O(logn)$

1
2
3
4
5
6
public void logarithm(int n) {
    int count = 1; // 执行一次
    while (count <= n) { // 执行logn次
        count = count*2; // 执行logn次
    }
}

该段代码什么时候会停止执行呢？是当count大于n时。也就是说多少个2相乘后其结果值会大于n，即$2^x=n$。由$2^x=n$可以得到$x=logn$，所以这段代码时间复杂度是$O(logn)$。

则对数底数大于 1 的象限通用表示为：

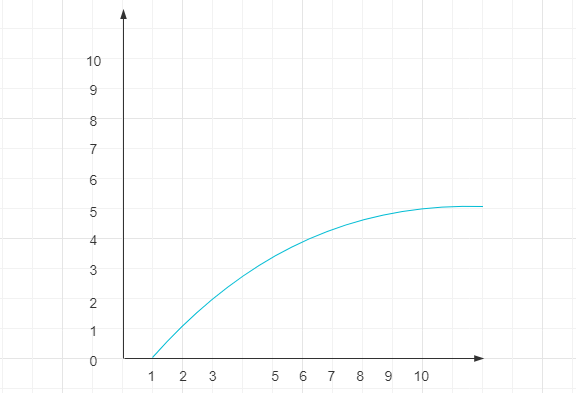
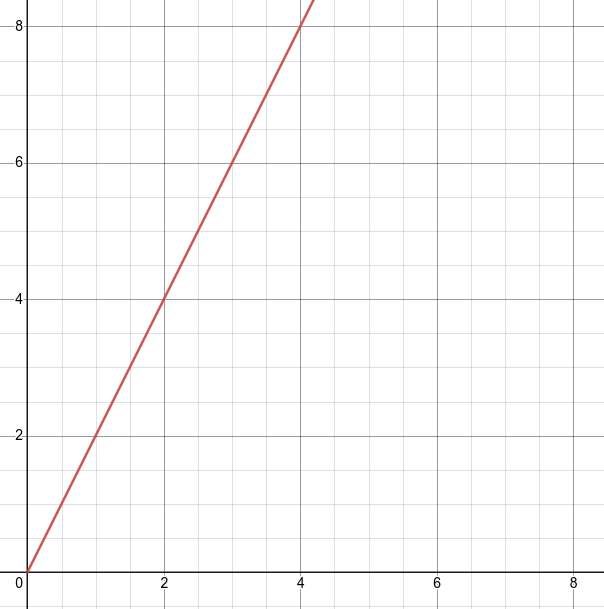
2.2.3 线性阶 $O(n)$

线性阶表示代码要执行n次，如下for循环中的代码，第二行和第三行代码都执行n次，即f(n)=2n。根据前面的分析，与最高次项相乘的常数2是可以忽略的，因此这段代码的时间复杂度是O(n)。

1
2
3
4
5
public void circle(int n) {
    for(int i = 0; i < n; i++) { // 执行n次
        System.out.println(i); // 执行n次
    }
}

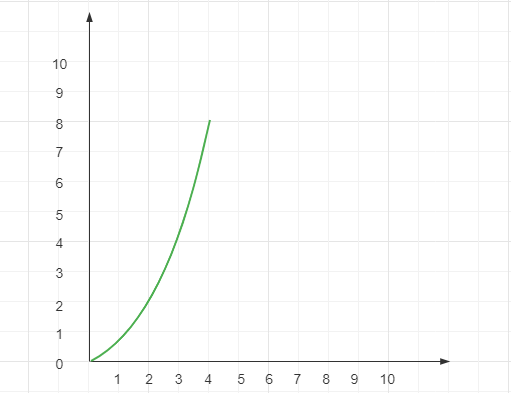
2.3.4 线性对数阶$ O(nlogn)$

线性对数阶$O(nlogn)$就是将一段时间复杂度为$O(logn)$的代码执行n次，如下代码所示。

1
2
3
4
5
6
7
8
public void logarithm(int n) {
    int count = 1;
    for(int i = 0; i < n; i++) { // 执行n次
        while (count <= n) { // 执行logn次
            count = count*2; // 执行nlogn次
        }
    }
}

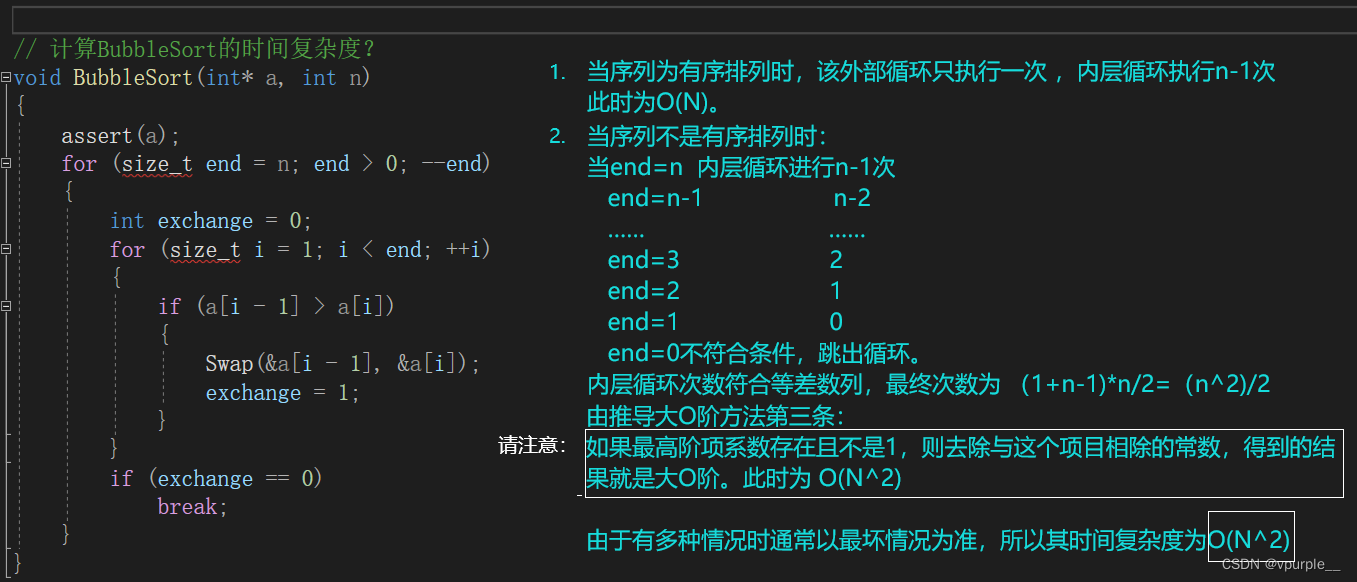
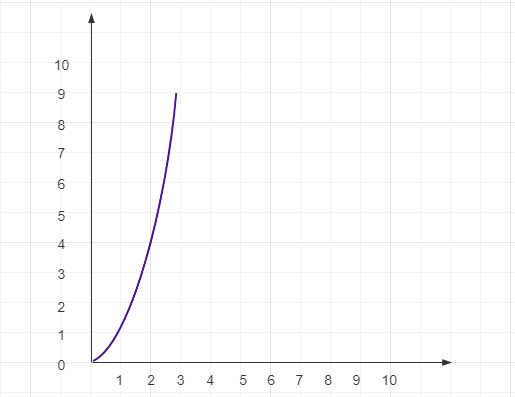
2.3.5 平方阶$ O(n^2)$

如下代码是个双重for循环，其内循环的时间复杂度是线性阶$O(n)$。对于外循环来说，是将内循环这个时间复杂度为$O(n)$代码在执行n次，所以整个这段代码的时间复杂度为$O(n^2)$。

1
2
3
4
5
6
7
public void square(int n) {
    for(int i = 0; i < n; i++){ // 执行n次
        for(int j = 0; j <n; j++) { // 执行n次
            System.out.println(i+j); // 执行n方次
        }
    }
}

2.3 常见时间复杂度计算举例

附录：